Dairy Processing

20 Clarification and Cream Separation

Centrifugation

Centrifugal separation is a process used quite often in the dairy industry. Some uses include:
  • clarification (removal of solid impurities from milk prior to pasteurization)
  • skimming (separation of cream from skim milk)
  • standardizing
  • whey separation (separation of whey cream (fat) from whey)
  • bactofuge treatment (separation of bacteria from milk)
  • quark separation (separation of quarg curd from whey)
  • butter oil purification (separation of serum phase from anhydrous milk fat)

Principles of Centrifugation

Centrifugation is based on Stoke’s Law. The particle sedimentation velocity increases with:

  • increasing diameter
  • increasing difference in density between the two phases
  • decreasing viscosity of the continuous phase

If raw milk were allowed to stand, the fat globules would begin to rise to the surface in a phenomena called creaming. Raw milk in a rotating container also has centrifugal forces acting on it. This allows rapid separation of milk fat from the skim milk portion and removal of solid impurities from the milk.

Clarification

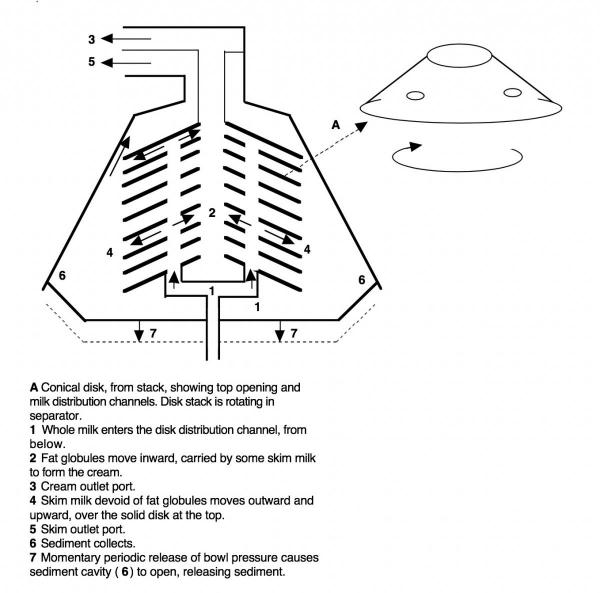
Separation and clarification can be done at the same time in one centrifuge. Particles, which are more dense than the continuous milk phase, are thrown back to the perimeter. The solids that collect in the centrifuge consist of dirt, epithelial cells, leukocytes, corpuscles, bacteria sediment and sludge. The amount of solids that collect will vary, however, it must be removed from the centrifuge.

More modern centrifuges are self-cleaning allowing a continuous separation/clarification process. This type of centrifuge consists of a specially constructed bowl with peripheral discharge slots. These slots are kept closed under pressure. With a momentary release of pressure, for about 0.15 s, the contents of sediment space are evacuated. This can mean anywhere from 8 to 25 L are ejected at intervals of 60 min. For one dairy, self-cleaning translated to a loss of 50 L/hr of milk.

The following image is a schematic of both a clarifier and a separator.

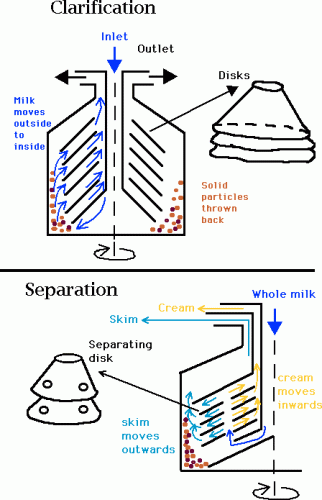
Diagram of Clarification and Separation

Separation

Centrifuges can be used to separate the cream from the skim milk. The centrifuge consists of up to 120 discs stacked together at a 45 to 60 degree angle and separated by a 0.4 to 2.0 mm gap or separation channel. Milk is introduced towards the inner edge of the disc stack. The stack of discs has vertically aligned distribution holes into which the milk is introduced.

Under the influence of centrifugal force the fat globules, which are less dense than the skim milk, move inwards through the separation channels toward the axis of rotation. Some skim is needed to carry the fat globules out of the separation, and the combination of fat globules in a much-reduced volume of skim milk is called “cream”, i.e., cream is skim milk enriched in fat globules. The skim milk, now devoid of fat globules, will move outwards and leaves through a separate outlet.

 

 

Standardization
Diagram explaining the automatic standardization process

The streams of skim and cream after separation must be recombined to a specified fat content. This can be done by adjusting the throttling valve of the cream outlet; if the valve is completely closed, all milk will be discharged through the skim milk outlet. If the valve is very slightly opened, you get most of the fat globules in a very small volume of skim, so cream with a high fat content. As the valve is progressively opened further, larger volumes of skim push the fat globules out, so you get larger volumes of cream but with diminishing fat contents (%) being discharged from the cream outlet. With direct standardization the cream and skim are automatically remixed at the separator to provide the desired fat content (see the diagram above to explain the automatic standardization process) . Some basic standardization problems including mass balance and Pearson square approach can be viewed on the following page.

Standardization Problems

Here are the two examples of how to do milk standardization calculations:

1. If a dairy has 160 kg of 40% fat cream and wishes to standardize it to 32% fat cream, how much skim milk (0% fat) must be added?

Mass Balance Approach

let x = kg skim milk

y = kg of 32% cream

Mass Balance Equation (total mass into the process = total mass out of the process) 160 + x = y

Component Balance for Fat (fat into the process = fat out of the process)

.40 (160) = .32 (y) which says 40% of 160 kg comes in and 32% of y goes out
.40 (160) = .32(160+ x), substituting our equation for y
.32x = 64 – 51.2
x = 40 kg skim milk

2. How much cream testing 35% fat must be added to 500 kg of milk testing 4% fat to obtain cream testing 10% fat?

Mass Balance Approach

let x = kg 35% cream

y = kg of 10% cream

Mass Balance x + 500 = y (mass in = mass out)

Component Balance for Fat

x (.35) + 500 (.04) = y (.10) again, fat in = fat out
x (.35) + 20 = x(.10) + 50
.25 x = 30
x = 120 kg of 35% cream

Note: if your algebra skills are not very good, I can highly recommend this website – I Do Maths.

Pearson square approach to above problem

A shortcut for 2-component mass balances
Place desired percentage in the centre of a rectangle
Place percentage composition of two available streams in left corners of rectangle
Cross subtract lower from higher numbers for right corners of triangle (higher number – lower number)
Use right corners as ratios of two streams

Using the above problem:

Component Mass
35     6
10
4     25        500
___     ____
31

35% cream = (500 x 6)/25 = 120 kg
This will produce 620 kg cream at 10% fat.

Check your work – (620 x 0.10) = (120 x .35) + (500 x .04) – correct!

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Dairy Science and Technology eBook Copyright © by H. Douglas Goff; Arthur Hill; and Mary Ann Ferrer is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book