Ice Cream Structure
29 Theoretical Aspects of the Freezing Process
The Process of Crystallization
This section will briefly review the physico-chemical processes that occur during a freezing process. The figure below shows the time-temperature relationship for freezing of pure water (ABCDE) and aqueous solutions (AB’C’D’). The first thermal event that can be seen from such a diagram is undercooling below the freezing point before the induction of crystallization, from A to B or B’ . This is a non-equilibrium, metastable state which is analogous to an activation energy necessary for the nucleation process. Pure water can be undercooled by several degrees before the nucleation phenomenon begins.
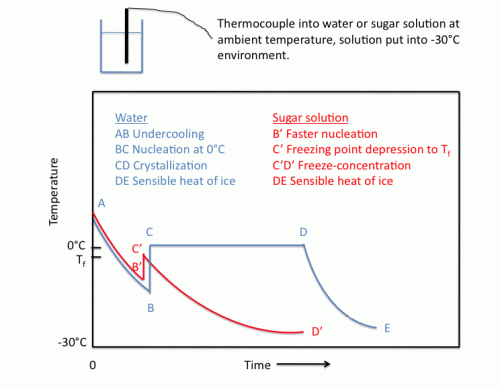
Once the critical mass of nuclei is reached, the system nucleates at point B or B’ in the figure and releases its latent heat faster than heat is being removed from the system. In aqueous solutions, however, B’ is not as low as B, since the added solute will promote heterogeneous nucleation, thereby accelerating the nucleation process. The temperature increases instantly to the initial freezing temperature of the solution at Point C (0oC) or C’ (Tf). The presence of solutes results in depression of the freezing point based on Raoult’s Law, which relates vapor pressure of the solution to that of pure solvent based on solute concentration. Note that C’ is not as high as C, because the initial freezing point is depressed as a result of the solute. Hence, the solute has greatly decreased the amount of undercooling for two reasons: faster nucleation and lowered freezing point. In very concentrated solutions, it is sometimes even difficult to induce undercooling.
In pure water, the time line from C to D in the figure reflects the time during which crystal growth is occurring at 0oC. Fast freezing rates promote the formation of many small ice crystals during this period. The partially frozen mixture will not cool until all of the “freezable” water has crystallized; hence, the line CD for pure water occurs at constant temperature. The freezing time is usually defined as the time from the onset of nucleation to the end of the crystal growth phase. After crystallization is completed, the temperature drops from D to E as sensible heat of ice is removed.
During the freezing of the aqueous solution, a freeze-concentration process occurs as water freezes out of solution in the form of pure ice crystals (C’D’), effectively removing solvent from the solute. Hence the freezing temperature of the remaining solution continues to drop. At temperatures well below the initial freezing point, some liquid water remains. Also, a large increase in the viscosity of the unfrozen phase occurs, thus decreasing the diffusion properties of the system and hindering crystallization. It is more difficult to assign a freezing time to this process, but it is usually taken as the time to reach some predetermined temperature below the initial freezing point. This freeze-concentration process establishes the freezing curve.
Importance of Crystallization Rate
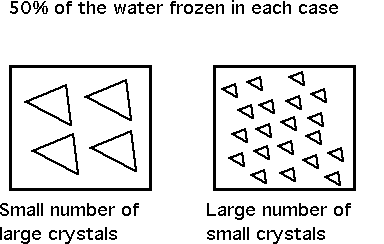
The freezing curve predicts the amount of ice at any given temperature, which is a function of freezing point depression and hence the number of solutes (concentration of sugar, etc.). It doesn’t predict anything about ice crystal size. What predicts ice crystal size is the rate of freezing – the faster the rate – the more nucleation is promoted, and the greater number of crystals of smaller size that will result. This is very important in terms of ice cream structure.
Mechanisms of ice recrystallization
Ice crystals formed after scraped-surface freezing and hardening of ice cream are unstable and will undergo recrystallization, the extent of which depends in part on how effectively the system has been stabilized. See also the discussion regarding ice cream shelf-life, where I have included some images to show the effects of recrystallization on ice crystals in ice cream. Recrystallization is the process of changes in number, size and shape of ice crystals during frozen storage, although the amount of ice stays constant with constant temperature throughout this process (dictated by the equilibrium freezing curve). Recrystallization basically involves small crystals disappearing, large crystals growing and crystals fusing together.
There are several types of recrystallization processes. Iso-mass recrystallization (“rounding off”) refers to changes in surface or internal structure so that crystals with irregular shapes and large surface-to-volume ratios assume a more compact structure. In other words, sharper surfaces are less stable than flatter ones and will show a tendency to become smoother over time. Migratory recrystallization refers in general to the tendency of larger crystals to grow at the expense of smaller crystals. Ostwald ripening refers to migratory recrystallization that occurs at constant temperature and pressure due to differences in surface energy between crystals, most likely involving melting-diffusion-refreezing or sublimation-diffusion-condensation mechanisms. However, migratory recrystallization is greatly enhanced by temperature fluctuations (heat shock) inducing a melt-refreeze behavior due to ice content fluctuations. Melt-refreeze behavior can lead to complete disappearance of smaller crystals during warming and growth of larger crystals during cooling, or to a decrease in size of crystals during partial melting and regrowth of existing crystals during cooling. Melt-refreeze should occur to a greater extent at higher temperatures and more rapidly for smaller crystals. Accretion refers to a natural tendency of crystals in close proximity to fuse together; the concentration gradients in the areas between them are high, thus, material is transported to the point of contact between crystals and a neck is formed. Further “rounding off” will occur because a high curvature surface like this has a natural tendency to become planar.
Formation of the Glassy Phase in Frozen Foods
During the freezing of foods, ice is formed as pure water goes through the two-step (nucleation and propagation) crystallization process. As temperature decreases and water is removed from a food in the form of ice, the solutes present in the UFP are freeze-concentrated. An equilibrium freezing temperature exists for each ice/UFP ratio, which is a function of the solute concentration. This equilibrium thermodynamic process can be modelled on a phase diagram as an equilibrium freezing (liquidus) curve (see figure below), which extends from the melting temperature (Tm) of pure water (0oC) to the eutectic temperature (Te) of the solute, the point at which the solute has been freeze-concentrated to its saturation concentration.
As temperature is lowered, it is highly unlikely that solute will crystallize at Te, due to high viscosity from concentration of solute and low temperature, so that freeze-concentration proceeds beyond Te in a non-equilibrium state. The highly-concentrated UFP can then go through a viscous liquid/glass state transition, driven by the reduction in molecular motion and diffusion kinetics as a result of both the very high concentration and low temperature.
A glass is defined as a non-equilibrium, metastable, amorphous, disordered solid of extremely high viscosity (ie., 10 exp10 to 10 exp14 Pa.s), also a function of temperature and concentration. The glass transition curve extends from the glass transition temperature (Tg) of pure water (-134oC) to the Tg of pure solute. The equilibrium phase diagram and the kinetically-derived state diagram can be modelled together on a supplemented state diagram. The supplementary state diagram showing the solid/liquid coexistence boundaries and glass transition profile for a binary sucrose/water system is shown in the figure below. Below and to the right of the glass transition line, the solution is in the amorphous glass state, with or without ice present depending on temperature and freezing path followed, while above and to the left of the glass transition line, the solution is in the liquid state, with or without ice depending on temperature.
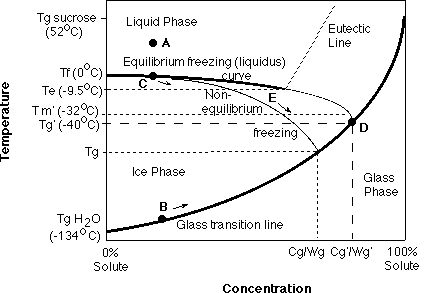
As an example, assume a sucrose solution with an initial concentration of 20% at room temperature (point A). The initial Tg of this solution at room temperature before phase separation is marked as point B (if the solution could be undercooled to this temperature without ice formation). However, upon slowly cooling of the system somewhat below its equilibrium freezing point (due to undercooling), nucleation and subsequent crystallization begins at point C and initiates the freeze-concentration process, removing water in its pure form as ice. As ice crystallization proceeds, the continual increase in solute concentration (removal of water) further depresses the equilibrium freezing point of the UFP in a manner which follows the liquidus curve (shown as path C) while the Tg of the UFP moves up the glass transition line (path B; due to increased concentration) with a rapid increase in viscosity in a non-Arrhenius manner, particularly in late stages of the freezing process.
Co-crystallization of solute at the Te is unlikely and thus freeze-concentration continues past Te into a non-equilibrium state since the solute becomes superstaurated. When a critical, solute-dependent concentration is reached, the unfrozen liquid exhibits very resisted mobility and the physical state of the UFP changes from a viscoelastic liquid to a brittle, amorphous solid glass.
The intersection of the non-equilibrium extension of the liquidus curve, beyond Te, and the kinetically-determined glass transition curve, point D in the above figure, represents the solute-specific, maximally freeze-concentrated Tg of the frozen system, denoted Tg’, where ice formation ceases within the time-scale of the measurement. The corresponding maximum concentrations of water and sucrose “trapped” within the glass at Tg‘ and unable to crystallize are denoted the Wg‘ and Cg‘ , respectively. It is worth noting that this unfrozen water is not bound in an “energetic” sense, rather unable to freeze within practical time frames.
At the Tg‘, the supersaturated solute takes on solid properties because of reduced molecular motion, which is responsible for the tremendous reduction in translational, not rotational, mobility. It is this intrinsic slowness of molecular reorganization below Tg‘ that the food technologist seeks to create within the concentrated phase surrounding constituents of food materials.
However, warming from the glassy state to temperatures above the Tg‘ results in a tremendous increase in diffusion, not only from the effects of the amorphous to viscous liquid transition but also from increased dilution as melting of small ice crystals occurs almost simultaneously (Tg‘ = Tm‘). The time-scale of molecular rearrangement continually changes as the Tg is approached, so that food technologists can also gain some enhanced stability at temperatures above Tg‘ by minimizing the delta T between the storage temperature and Tg‘ , either by reduced storage temperatures or enhaced Tg‘ through freezing methods or formulation. Hence, knowledge of the glass transition provides a clear indication of molecular diffusion and reactivity, and therefore, shelf-stability.
Formation of a Dilute Glass
Despite the thermodynamic driving force to achieve the unfrozen water content corresponding to Wg’, one must also consider the large kinetic factors which “overtake” the freezing process. At sub-zero temperatures, the formation of an amorphous state is time-dependent since the limiting factor of the process (water removal in the form of ice) becomes more difficult as concentration increases. The exponential effect of viscosity on mass transfer properties acts as the limiting factor for growth. In addition, under conditions where heat removal is rapid, a high level of undercooling at the interface will only add to a further decrease in propagation rate. The net result is that freezing becomes progressively slower as ice crystallization is hindered and consequently more time is required for lattice growth at each temperature.
Therefore the kinetic restriction imposed on the system can lead to a situation in which non-equilibrium freezing, resulting in a partial dilute glass, can occur. The typical pathway a system may follow during non-equilibrium freezing is shown in the figure on the previous page as the line leading to lower Tg (path E) than Tg‘ with a corresponding lower sucrose concentration in the glass (Cg) and higher water content in the glass (Wg) due to excess undercooled water plasticized within the glass. This is often referred to as a dilute glass. The magnitude of deviation from the equilibrium curve, and hence the actual path followed, may be regarded as a function of the degree of departure from equilibrium.
Systems possessing this undesirable structure may undergo various relaxation-recrystallization mechanisms in order to maximally freeze-concentrate and minimize the unfrozen water content. As a result, during warming, systems formed under these conditions may lead to one or more low temperature transitions, followed by an exothermic devitrification peak due to crystallization of immobilized water, and finally the onset of ice melting, Tm.

