The foundations of bioelectricity are two-fold: diffusion (which is governed by chemical and electrical gradients) and the semi-permeable membrane (which creates a separation of charge). In this section, we will explore the membrane potential of a cell at rest. We will also look at two equations that are used to calculate resting membrane potential. Remember: the resting membrane potential of a neuron is about −70 millivolts (mV). This means that the inside of the neuron is 70 mV less than the outside. Now, let’s find out why!

Resting Membrane Potential

Remember that the cell membrane consists of a phospholipid bilayer decorated with a variety of different ion channels. The cell membrane has an electrical state, called the membrane potential. This is the difference in total charge between the outside and inside of the cell. Although it varies between cells, the most commonly used value for resting membrane potential is −70mV.

The following video explains how diffusion and electrostatic forces dictate the movement of ions across the cell membrane. It also explains why different ions have different equilibrium potentials. This short video is a great starting point for understanding why the cell membrane is −70 mV at rest. At 1:00 equilibrium potentials are discussed while at 3:15 resting membrane potential of −70mV is reviewd.

Did you know diffusion has a specific rate at which molecules move? If you stepped on a tack, you would need that information to move from your foot to your spinal cord, and back down your foot. This would take around 112 days for that signal to travel by diffusion. The fastest way for information to move is with bioelectricity (the movement of ions). It is only possible because our plasma membranes are semi-permeable, allowing the setup of separation of charge.

Why is the resting membrane potential −70mV?

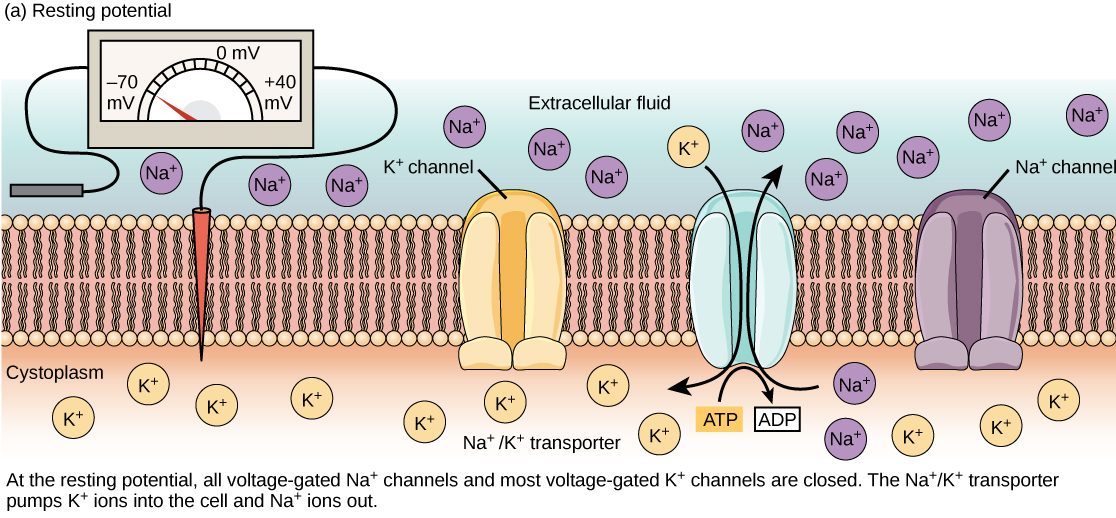
At rest (when most ion channels are closed), the concentration of sodium ions (Na⁺) is greater outside the cell, and the concentration of potassium ions (K⁺) is greater inside the cell. This is because the cell possesses K⁺ and Na⁺ leak channels that allow the two cations to diffuse down their concentration gradient. However, neurons have far more potassium leakage channels than sodium leakage channels. Therefore, K⁺ diffuses out of the cell at a much faster rate than sodium leaks in. Because more cations are leaving the cell than are entering, a difference in charge forms leaving the interior of the cell negatively charged relative to the outside of the cell.

The actions of the sodium-potassium pump help to maintain the resting potential, once established. Recall that the sodium-potassium pump brings two K⁺ ions into the cell while removing three Na⁺ ions per ATP consumed. As more cations are expelled from the cell than taken in, the inside of the cell remains negatively charged relative to the extracellular fluid.

The following diagram shows the ions that are responsible for setting up the resting membrane potential, and on which side of the plasma membrane they are found. The diagram is also useful because shows the various transporters and channels responsible for setting up the resting membrane potential.

Ever wonder how electric eels generate such high levels of electricity? Eels have specialized cells called electrocytes that can generate a charge of up to 600V to stun prey and keep predators away!

The following activity provides a visual experience that highlights which ions are more concentrated inside versus outside of the cell. Potassium ions (K⁺), chloride ions (Cl⁻), and sodium ions (Na⁺) all exist within our bodies. Which ions are more concentrated outside of the cell? What about inside the cell? Drag the appropriate ions to where they exist in a higher concentration (either outside or inside of the cell below). It is crucial to understand this fundamental concept in order to move onto subsequent chapters.

The Nernst equation is used to calculate the electrical potential across a membrane when the membrane is permeable to a single ion. The equation is used to calculate E, which is the equilibrium potential (V_eq) for a given ion, usually stated in millivolts (mV). T is the temperature in Kelvin (K = °C + 273.15) and Z is the valence of the ionic species, and is unitless. For example, z is +1 for Na⁺, +1 for K⁺, +2 for Ca²⁺, etc. F is Faraday’s constant (96484.56 C/mol), ln is natural log, and [ion]i/o is the concentration of the ionic species X in the intracellular (i) or extracellular (o) fluid.

This Nernst Equation Calculator, allows you to insert values and calculate the equilibrium potential of different ions. This is a great resource if you need extra practice! It is important to note the Nernst equation is useful to determine whether or not the intracellular concentration of an ion is above or below its electrochemical potential. In reality, the Nernst equation does not give a very good estimate of membrane potential because cells are permeable to other ions. 

The Goldman Equation

If two or more ions contribute to the membrane potential (V_m), we use the Goldman equation. In real life, K⁺, Na⁺, and Cl⁻ are the major contributors to the resting membrane potential of a cell. The equation is also used to calculated E, which is the membrane potential (V_m), usually stated in millivolts (mV). R is the universal gas constant (8.31441 J/mo/K), T is the temperature in Kelvin (K = °C + 273.15), F is Faraday’s constant (96484.56 C/mol) and ln is natural log. p_K/Na/Cl are the relative membrane permeabilities for K⁺, Na^+, and Cl^–. If no channels for s specific ion are open, the relative permeability is equal to zero. Note that a typical neuron at rest sits at p_K = 1, p_Na = 0.05, p_Cl = 0.45, while a typical neuron at the peak of an action potential sits at p_K = 1, p_Na = 12, p_Cl = 0.45. As you continue to read below, ask yourself why the relative permeability of sodium changes so drastically? Lastly, K⁺/Na⁺/Cl^–]_i/o are the concentrations of the ion in the intracellular (i) and extracellular (o) fluid.

[latex]E = \frac{RT}{F} ln \frac{pK[K^+]_O + pNa[Na^+]_O + pCl[Cl^-]_i}{pK[K^+]_i + pNa[Na^+]_i + pCl[Cl^-]_O}[/latex]

This Goldman Equation Calculator, allows you to insert values to see how ions are contributing to membrane potential. This is a great resource if you need extra practice!

The following video provides a good summary of the bioelectricity section. Don’t focus on memorizing any of the numbers or equations. Rather, focus on understanding the factors that contribute to a single ion’s equilibrium potential, and how all of these ions influence the resting membrane potential of a cell.

Are some of these concepts still not clicking? Try watching this video on Bioelectrical Calculations.

Subchapter Quiz

The questions below can be used to assess your knowledge within this chapter. There are five multiple-choice questions that you should attempt without referring to your notes. The questions will provide you with responses to your answers to guide your studying but should not be used as your only resource.